Matrix Essentials

So a quick reminder - what is a matrix? A matrix is just a grid of numbers. We usually describe them by talking about a "3x2 matrix", indicating that we're talking about a grid of numbers with 3 rows and 2 columns.

We use them non-stop in 3D graphics as they are a very neat and efficient way to perform certain calculations. It's difficult for me to stress how powerful they are right now until we get into transformation matrices, when hopefully this will become clear, so for now you'll have to take my word for it. The other side of things is that due to their utility, graphics cards have become extremely optimised for working with matrices. That is how it expects you to do your transformations, and to get the most power and speed from your graphics card you should follow these expectations.

The core idea of the matrix in graphics is that you can multiply any 3D coordinates by them, and the result will be another set of 3D coordinates with some transformation applied. Think scaling, translating, rotating, etc. We can also multiply two matrices together, which has the affect of combining these two transformations.

We often perform matrix multiplication, but unlike regular numbers, we don't really add, subtract or divide matrices. Multiplying them is all you will need!

Matrix Multiplication

So how do we multiply matrices? Let's start by multiplying two 2x2 matrices together:

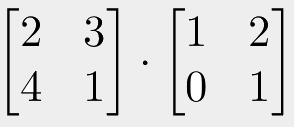
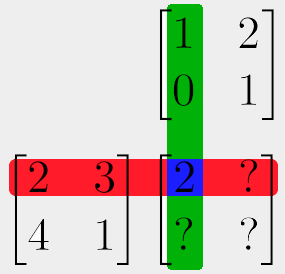
An easy way to imagine the multiplication is to place the the two matrices we wish to multiply along the edge of the "result" matrix like this:

So that matrix with the question marks is the result of multiplying the other two together.

To actually calculate the individual values of the resulting matrix, we start by taking the top-most value from the same column, and the left-most value from the same row. We multiply these together. Then we take the second-from-top value in the column, and second-from-left value in the row, and multiply these together. Then we take all our multiplied values and sum them together to get our result:

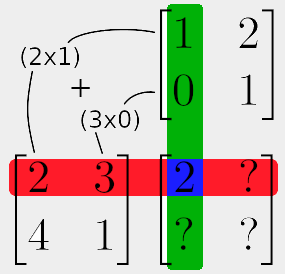
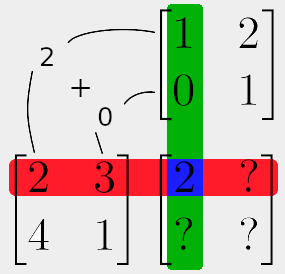
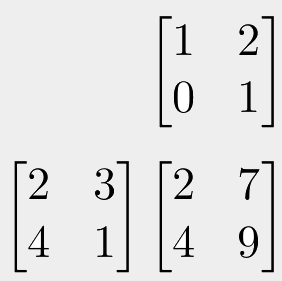
Working through this example, to get the top-left value in our result matrix, we multiply the first values from the same row and column (2 x 1 = 2). We do the same for the second value (3 x 0 = 0). Finally, we add these numbers together to get the top-left value of our result matrix (2 + 0 = 2).

To calculate the bottom-left value of the result matrix, again we multiply the first value in that column and row (4 x 1 = 4) and then add it to the second value in each row and column (1 x 0 = 0). The sum then comes out as 4, giving us our value for the bottom-left value. We can then carry this on to get the values for the rest of our result matrix.

If we are instead multiplying two 3x3 matrices together, it works exactly the same. Take the first value in each row and column and multiply them. Then do the same for the second values. Then there will now be a 3rd value in each row and column, so multiply those too. Then just sum the three totals.

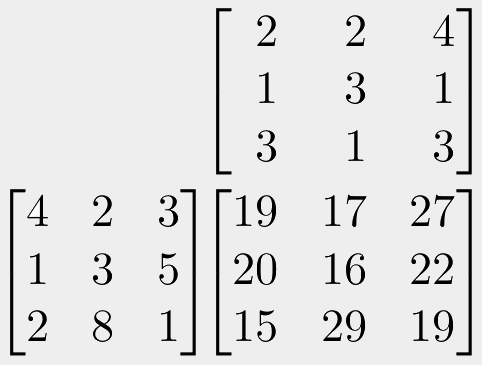
In this example, the top-left most value of the result matrix can be calculated as (4 x 2 = 8) for the first value, (2 x 1 = 2) for the second, and (3 x 3 = 9) for the third value. Summing 8 + 2 + 9 gives us the total of 19.

The same thing happens when we matrix multiply (called "matmul" for short) a vector with a matrix:

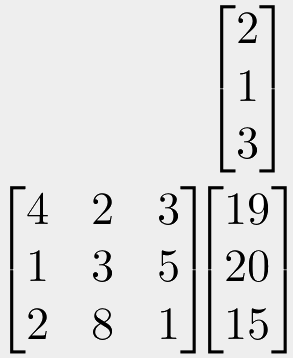
The result of multiplying a vector with a matrix is another vector. This implies that multiplying a set of coordinates by a transformation matrix will give us another set of coordinates, with the transform applied.

You may have realised at this point that the shape of the result matrix is therefore determined by the shape of what is being multiplied. The result will have the same number of rows as the first matrix, and the same number of columns as the second.

But what happens if we flip the calculation? What happens if we multiply the 3x3 matrix by a vector?

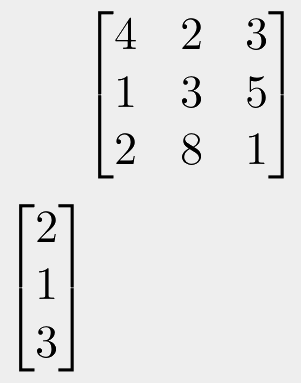
To calculate the top left value of the result, we would need to multiply the 4 from the top of the column with the first value in the row. So let's go with the 2 as being the first value in the same row. But then what do we multiply the 1 with to get the second value? There are no more values in the same row!

The answer is that this is not defined. You cannot multiply these matrices together. And not in the same sense of "you technically cannot divide by zero, but we can pretend zero = 0.00001 to make our maths play nicely". Here it is really undefined, you cannot do it. You should not do it. It means your logic is wrong.

A simple way to see if two matrices are multiply-able is to look at their sizes. Let's imagine we are multiplying a 3x3 matrix by a 3x1 matrix. For these two sizes, the inner two values (both 3) must be the same. If they are, you can imagine they cancel out, and what we are left with is the size of the result matrix. In this case if we cancel out our middle values: 3x3 and 3x1, we are left with a result of size 3x1. If they cannot be cancelled out, you cannot calculate the result's size, and therefore a result cannot be calculated either.

This implies that matrix multiplication is non-commutative. Normally, in regular mathematics, the numbers 2 and 5 can be multiplied either way round. 2x5 is the same as 5x2, and it makes no difference which we round we do it. So we say regular multiplication is commutative, you can freely change the order of the inputs and get the same result.

But for matrices, this is not true. Flipping the order of the inputs can give you a different matrix with a different size! Or it may not be possible to calculate at all! The above example of multiplying a 3x3 matrix by a 3x1 matrix flipped around becomes a 3x1 matrix multiplied by a 3x3 matrix. As the inner numbers are different, this is not possible! So do not forget! The order that you multiply matrices together is extremely important! You are not free to re-order your equations!