Cross Product

What is it?

Let's say you have two directional vectors. They both point from the origin in any two directions in 3D space. Logically, there must be a plane which both of these two vectors lay on. If your struggling to imagine that, point both your arms in any two directions. There is some flat 2D plane which both of these arms lie flat on.

What the cross product gives us is a third vector which is perpendicular to this plane. It gives us a vector which is guaranteed to be a 90° to both of the two original vectors.

Because the new vector is perpendicular to the plane, we can also say it is a normal vector of the plane. This normal vector points in the direction of the "third dimension" relative to this plane. Therefore cross products are defined in 3D, but not for 2D. If we imagine a flat sheet of paper on a table is our plane. Then the cross product would give us a vector pointing directly upwards or down. That's its main purpose.

This is an incredibly useful purpose though. It's used a huge amount, because it can be used to calculate the normals of triangles.

So when I said imagine a sheet of paper, let's take its 3D vertices at the corners. From any starting corner, travel along the edge to the nearest vertex to the left and right. If you subtract the initial vertex from each, these effectively give you two directional vectors aligned to the paper. We can then normalise each of them, and calculating the cross product will give us a normalised directional vector, which is the normal of our paper. Normal vectors then allow you to calculate your angle of incidence for lighting and reflections, so these are incredibly important.

Calculation

The formula for calculating the cross product is not pretty, but let's have a look.

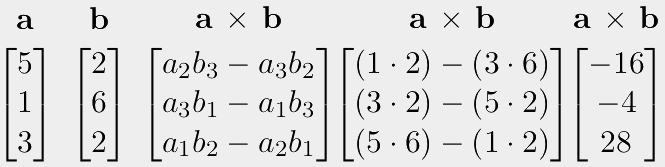
We start with our two vectors, a and b, on the left. The cross product of a and b is usually denoted with the cross or "x" symbol. I don't want to get into the proof of the formula for the cross product, it is available on Wikipedia if you want to read further into it. However the formula amounts to multiplying the various pairs of values from the vectors, and then subtracting other pairs.

So the first value is calculated by multiplying the second value in a with the third value in b, and then subtracting the third value in a multiplied by the second value in b. But don't worry, you don't need to remember this. Certainly not the equations. Just remember that the cross product gives you a vector that is at a right-angle to both the two input vectors.

Edge Cases

Worth noting is that while we get a vector which is perpendicular to both of the original vectors, there are actually two possible vectors which fit this criteria. There is one pointing above the plane, and one pointing below. So which one does the cross product give us?

Well conveniently the cross product follows the right-hand rule like OpenGL uses. If you point your thumb and first finger along the lines of a and b, then your middle finger will point in the direction of the cross product. This is one of the reasons why the winding order is important in OpenGL, as if we flip the input vectors of the cross product, we get the perpendicular vector pointing in the other direction.

If you want the other vector anyway, don't forget you can just take the cross product result and invert it, by flipping the sign on each component.

Of course the choice of which of the two perpendicular vectors the cross product gives us is only by convention. You can rewrite the formula to use different "pairs" to get the left-handed cross-product if you really wanted to. But you really shouldn't do that as it will confuse everyone else who ever sees your code! Conventions exist for a reason!

One more thing to note is that the plane is not defined if both our vectors are pointing in exactly the same direction (or the same but opposite directions). If you cross product these vectors, you will get a zero vector as a result (all zeroes), basically meaning the result is undefined. This makes sense if you consider that there are infinitely many directional vectors that are at a right-angle to a line in 3D.

Once again though, don't feel like you need to remember how the cross product works. The key take away here is that for any two directional vectors, there is a mathematical function which will give us a third vector, which will be perpendicular (at a right angle) to both of the inputs. It will also be normalised if both the inputs are normalised. If they are not, you can always just normalise the result!